Python Algorithm and Data Structure

Posted on Edited on In Views: Symbols count in article: 35k Reading time ≈ 32 mins.

Python 数据结构与算法分析

各种算法和数据结构时间复杂度总结

Stack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Stack: 
    '''Last in First out, insert to last place'''
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []
    
    def push(self, item):
        self.items.append(item)
    
    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[-1]

    def size(self):
        return len(self.items)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Stack: 
    '''Last in First out, insert first place'''
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []
    
    def push(self, item):
        self.items.insert(0,item)
    
    def pop(self):
        return self.items.pop(0)

    def peek(self):
        return self.items[0]

    def size(self):
        return len(self.items)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == '(':
            s.push(symbol)
        elif s.isEmpty():
            balanced = False
        else:
            s.pop()
        index = index + 1
    if balanced and s.isEmpty():
        return True
    else:
        return False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol in '([{':
            s.push(symbol)
        elif s.isEmpty():
            balanced = False
        else:
            top = s.pop()
            if not matches(top, symbol):
                balanced = False
        index = index + 1
    if balanced and s.isEmpty():
        return True
    else:
        return False

def matches(open,close):
    opens = '([{'
    closes = ')]}'
    return opens.index(open) == closes.index(close)
1

Queue

1
2
3
4
5
6
7
8
9
10
11
class Queue:
    def __init__(self) -> None:
        self.items = []
    def isEmpty(self):
        return self.items == []
    def enqueue(self, item):
        self.items.insert(0,item)
    def dequeue(self):
        return self.items.pop()
    def size(self):
        return len(self.items)
1
2
3
4
5
6
7
8
9
10
11
def hotPotato(namelist, num):
    simqueue = Queue()
    for name in namelist:
        simqueue.enqueue(name)
    while simqueue.size()>1:
        for i in range(num):
            simqueue.enqueue(simqueue.dequeue())
        simqueue.dequeue()
    return simqueue.dequeue()

print(hotPotato([1,2,3,4,5,6,7,8],7))
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import random


class Printer:
    def __init__(self,ppm):
        self.pagerate = ppm
        self.currentTask = None
        self.timeRemaining = 0

    def tick(self):
        if self.currentTask != None:
            self.timeRemaining = self.timeRemaining - 1
            if self.timeRemaining <= 0:
                self.currentTask = None
    def busy(self):
        if self.currentTask != None:
            return True
        else:
            return False
    def startNext(self, newtask):
        self.currentTask = newtask
        self.timeRemaining = newtask.getPages() * 60/self.pagerate

class Task:
    def __init__(self, time) -> None:
        self.timestamp = time
        self.pages = random.randrange(1,21)
    def getStamp(self):
        return self.timestamp
    def getPages(self):
        return self.pages
    def waitTime(self, currenttime):
        return currenttime - self.timestamp
def newPrintTask():
    num = random.randrange(1,181)
    if num == 180:
        return True
    else:
        return False
def simulation(numSeconds, pagesPerMinute):
    labprinter = Printer(pagesPerMinute)
    printQueue = Queue()
    waitingtimes = []

    for currentSecond in range(numSeconds):
        if newPrintTask():
            task = Task(currentSecond)
            printQueue.enqueue(task)
        if (not labprinter.busy()) and (not printQueue.isEmpty()):
            nexttask = printQueue.dequeue()
            waitingtimes.append(nexttask.waitTime(currentSecond))
            labprinter.startNext(nexttask)
        labprinter.tick()
    averageWait = sum(waitingtimes)/len(waitingtimes)
    print(f'Average wait {averageWait:8.2f} secs {printQueue.size():3d} tasks remaining.')
1
2
for i in range(10):
    simulation(3600,5)
Average wait    49.06 secs   0 tasks remaining.
Average wait   129.56 secs   0 tasks remaining.
Average wait    29.47 secs   0 tasks remaining.
Average wait    76.53 secs   1 tasks remaining.
Average wait    57.75 secs   0 tasks remaining.
Average wait    17.36 secs   1 tasks remaining.
Average wait    99.14 secs   0 tasks remaining.
Average wait   253.56 secs   0 tasks remaining.
Average wait   115.83 secs   0 tasks remaining.
Average wait   265.00 secs   4 tasks remaining.

双端队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Deque:
    def __init__(self) -> None:
        self.items = []
    def isEmpty(self):
        return self.items == []
    def addFront(self, item):
        self.items.append(item)
    def addRear(self, item):
        self.items.insert(0,item)
    def removeFront(self):
        return self.items.pop()
    def removeRear(self):
        return self.items.pop(0)
    def size(self):
        return len(self.items)

内置库实现双端队列

1
from collections import deque

无序表

链表实现无序表

1
2
3
4
5
6
7
8
9
10
11
12
class Node:
    def __init__(self, initdata) -> None:
        self.data = initdata
        self.next = None
    def getData(self):
        return self.data
    def getNext(self):
        return self.next
    def setData(self, newdata):
        self.data = newdata
    def setNext(self,newnext):
        self.next = newnext

递归

1
2
3
4
# 调整sys最大递归深度
# import sys
# sys.getrecursionlimit()
# sys.setrecursionlimit()

无序表

用链表实现无序表：基本元素：节点
无序表本身不包含数据，只包含节点的引用
添加新数据最快的位置是head

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Node:
    def __init__(self, initdata) -> None:
        self.data = initdata
        self.next = None
    def getData(self):
        return self.data
    def getNext(self):
        return self.next
    def setData(self,newdata):
        self.data = newdata
    def setNext(self, newnext):
        self.next = newnext

class UnorderedList:
    def __init__(self) -> None:
        # head 对第一个节点的引用 
        self.head = None
    def add(self, item):
        temp = Node(item)
        temp.setNext(self.head)
        self.head = temp
    def size(self):
        current = self.head
        count = 0
        while current != None:
            count = count + 1
            current = current.getNext()
        return count
    def search(self, item):
        current = self.head
        found = False
        while current != None and not found:
            if current.getData() == item:
                found = True
            else:
                current = current.getNext()
        return found
    def remove(self,item):
        current = self.head
        previous = None
        found = False
        while not found:
            if current.getData() == item:
                found = True
            else:
                previous = current
                current = current.getNext()
        if previous == None:
            self.head = current.getNext()
        else:
            previous.setNext(current.getNext())



有序表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class OrderedList:
    def __init__(self) -> None:
        self.head = None
    def search(self, item):
        current = self.head
        found = False
        stop = False
        while current != None and not found and not stop:
            if current.getData() == item:
                found = True
            else:
                if current.getData() > item:
                    stop = True
                else:
                    current = current.getNext()
        return found
    def add(self, item): 
        current = self.head 
        previous = None 
        stop = False 
        while current != None and not stop: 
            if current.getData() > item: 
                stop = True 
            else: 
                previous = current 
                current = current.getNext() 
        temp = Node(item) 
        if previous == None: 
            temp.setNext(self.head) 
            self.head = temp 
        else: 
            temp.setNext(current) 
            previous.setNext(temp)
    # 剩下的操作幼自己写： size, remove

线性结构小结

  • stack：后进先出
  • Queue：先进先出
  • 双端队列：可以同时具备stack和queue的功能
  • 链表List：不需要连续存储空间，head需要特别处理
    • 无序表
    • 有序表

递归应用

重复计算太多， 可以记录中间结果

找零

1
2
3
4
5
6
7
8
9
10
def recMC(coinValueList, change):
    minCoins = change
    if change in coinValueList:
        return 1
    else:
        for i in [c for c in coinValueList if c<=change]:
            numCoins = 1 + recMC(coinValueList, change-i)
            if numCoins < minCoins:
                minCoins = numCoins
    return minCoins
1
recMC([1,5,10,25],63)
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def recDC(coinValueList, change, knownResults):
    minCoins = change
    if change in coinValueList:
        knownResults[change] = 1
        return 1
    elif knownResults[change] > 0:
        return knownResults[change]
    else:
        for i in [c for c in coinValueList if c<=change]:
            numCoins = 1 + recMC(coinValueList, change-i, knownResults)
            if numCoins < minCoins:
                minCoins = numCoins
                knownResults[change] = minCoins
    return minCoins
1
recDC([25,10,5,1], 63, [0]*64)
6

动态规划
从最简单的情况开始，递增寻找最优

1
2
3
4
5
6
7
8
9
def dpMakeChange(coinValueList, change, minCoins):
    for cents in range(1,change+1):
        coinCount = cents
        for j in [c for c in coinValueList if c<=cents]:
            if minCoins[cents-j]+1<coinCount:
                coinCount = minCoins[cents-j]+1
        minCoins[cents] = coinCount
    return minCoins[change]
    
1
dpMakeChange([1,5,10,21,25],63,[0]*64)
3

查找

顺序查找

无序表查找

1
2
3
4
5
6
7
8
9
10
def sequentialSearch(alist, item):
    pos = 0
    found = False
    while pos < len(alist) and not found:
        if alist[pos] == item:
            found = True
        else:
            pos = pos + 1
    return found

有序表查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def orderedSequentialSearch(alist, item):
    pos = 0
    found = False
    stop = False
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        else:
            if alist[pos] > item:
                stop = True
            else:
                pos = pos + 1
    return found

1
2
testlist = [0,1,2,3,4,5]
print(orderedSequentialSearch(testlist, 3))
True
1
print(sequentialSearch(testlist,8))
False

有序表，二分查找：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def binarySearch(alist, item):
    first = 0
    last = len(alist) - 1
    found = False

    while first<=last and not found:
        midpoint = (first + last)//2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
                last = midpoint - 1
            else:
                first = midpoint + 1
    return found
    
1
print(binarySearch(testlist,4))
True

递归实现二分法

1
2
3
4
5
6
7
8
9
10
11
12
13
def binarySearch(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint] == item:
            return True
        else:
            if item<alist[midpoint]:
                return binarySearch(alist[:midpoint], item)
            else:
                return binarySearch(alist[midpoint+1:], item)
                
1
binarySearch(testlist,3)
True

有序表查找也有排序的开销，有时候数据经常变动的话，不如用无序表和顺序查找更快

排序算法

冒泡排序
两两相邻交换，最大项交换到最后，经过n-1次

1
2
3
4
5
6
7
8
9
10
def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]

alist = [54,26,93,17,77,31,44,55,20]
bubbleSort(alist)
print(alist)

[17, 20, 26, 31, 44, 54, 55, 77, 93]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def shortBubbleSort(alist):
    exchanges = True
    passnum = len(alist)-1
    while passnum > 0 and exchanges:
        exchanges = False
        for i in range(passnum):
            if alist[i] > alist[i+1]:
                exchanges = True
                alist[i],alist[i+1] = alist[i+1], alist[i]
        passnum = passnum - 1

alist = [20,30,40,90,50,60,70,80,100,110]
shortBubbleSort(alist)
print(alist)

[20, 30, 40, 50, 60, 70, 80, 90, 100, 110]

选择排序

1
2
3
4
5
6
7
def selectionSort(alist):
    for fillslot in range(len(alist)-1,0,-1):
        positionOfMax = 0
        for location in range(1,fillslot+1):
            if alist[location]>alist[positionOfMax]:
                positionOfMax = location
        alist[fillslot], alist[positionOfMax] = alist[positionOfMax],alist[fillslot]
1
2
3
alist = [54,26,93,17,77,31,44,55,20]
selectionSort(alist)
print(alist)
[17, 20, 26, 31, 44, 54, 55, 77, 93]
1
2
3
4
5
6
7
8
9
def insertionSort(alist):
    for index in range(1,len(alist)):
        currentvalue = alist[index]
        position = index
        while position>0 and alist[position-1]>currentvalue:
            alist[position] = alist[position-1]
            position = position - 1
        alist[position] = currentvalue
    
1
2
3
alist = [54,26,93,17,77,31,44,55,20]
insertionSort(alist)
print(alist)
[17, 20, 26, 31, 44, 54, 55, 77, 93]

谢尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def shellSort(alist):
    sublistcount = len(alist)//2
    while sublistcount>0:
        for startposition in range(sublistcount):
            gapInsertionSort(alist, startposition, sublistcount)
        print('After increments of size',sublistcount,'The list is',alist)
        sublistcount = sublistcount // 2

def gapInsertionSort(alist,start,gap):
    for i in range(start+gap,len(alist),gap):
        currentvalue = alist[i]
        position = i
        while position>=gap and alist[position-gap]>currentvalue:
            alist[position] = alist[position-gap]
            position = position - gap
        alist[position] = currentvalue
    
alist = [54,26,93,17,77,31,44,55,20]
shellSort(alist)
print(alist)
After increments of size 4 The list is [20, 26, 44, 17, 54, 31, 93, 55, 77]
After increments of size 2 The list is [20, 17, 44, 26, 54, 31, 77, 55, 93]
After increments of size 1 The list is [17, 20, 26, 31, 44, 54, 55, 77, 93]
[17, 20, 26, 31, 44, 54, 55, 77, 93]
1
list(range(0,20,4))
[0, 4, 8, 12, 16]

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from turtle import left


def mergeSort(alist):
    if len(alist)>1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i= j= k= 0
        while i<len(lefthalf) and j<len(righthalf):
            if lefthalf[i]<righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i<len(lefthalf):
            alist[k] = lefthalf[i]
            i=i+1
            k=k+1
        
        while j<len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1
1
2
3
alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)
[17, 20, 26, 31, 44, 54, 55, 77, 93]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def mergeSort(lst):
    # 递归结束条件
    if len(lst)<=1:
        return lst

    # 分解问题， 并递归调用
    middle = len(lst)//2
    left = mergeSort(lst[:middle]) # 左半部排好序
    right  = mergeSort(lst[middle:]) # 右半部排好序
    
    # 合并左右半部，完成排序
    merged = []
    while left and right:
        if left[0] <= right[0]:
            merged.append(left.pop(0))
        else:
            merged.append(right.pop(0))
    merged.extend(right if right else left)
    return merged
1
2
3
alist = [54,26,93,17,77,31,44,55,20]

print(mergeSort(alist))
[17, 20, 26, 31, 44, 54, 55, 77, 93]

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from turtle import right


def quickSort(alist):
    quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
    if first < last:
        splitpoint = partition(alist,first,last)
        quickSortHelper(alist,first,splitpoint-1)
        quickSortHelper(alist,splitpoint+1,last)
def partition(alist,first,last):
    pivotvalue = alist[first]

    leftmark = first + 1
    rightmark = last

    done = False
    while not done:
        while alist[leftmark] <= pivotvalue and leftmark <= rightmark:
            leftmark = leftmark +1
        while alist[rightmark] >= pivotvalue and rightmark >=leftmark:
            rightmark = rightmark - 1
        if rightmark < leftmark:
            done = True
        else:
            alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
    
    alist[first], alist[rightmark] = alist[rightmark], alist[first]

    return rightmark

alist = [54,26,93,17,77,31,44,55,20]
quickSort(alist)
print(alist)
[17, 20, 26, 31, 44, 54, 55, 77, 93]

散列函数

MD5和SHA系列hash function: hashlib

1
2
import hashlib
hashlib.md5("hello world".encode('utf-8')).hexdigest()
'5eb63bbbe01eeed093cb22bb8f5acdc3'
1
2
m = hashlib.md5()
m.update('hello world'.encode('utf-8'))
1
2
print(m)
print(m.hexdigest())
<md5 _hashlib.HASH object @ 0x000002345866C390>
5eb63bbbe01eeed093cb22bb8f5acdc3
1
m.update('nihao shijie'.encode('utf-8'))
1
2
print(m)
print(m.hexdigest())
<md5 _hashlib.HASH object @ 0x000002345866C390>
215aa34b159e42f10d53a1187363b520

冲突解决方案：开放定址（线性探测linear probing）

树

嵌套列表表示树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def BinaryTree(r): 
    return [r, [], []]
def insertLeft(root, newBranch): 
    t = root.pop(1) 
    if len(t) > 1: 
        root.insert(1, [newBranch, t, []]) 
    else: 
        root.insert(1, [newBranch, [], []]) 
    return root
def insertRight(root, newBranch): 
    t = root.pop(2) 
    if len(t) > 1: 
        root.insert(2, [newBranch, [], t]) 
    else: 
        root.insert(2, [newBranch, [], []]) 
    return root
def getRootVal(root): 
    return root[0] 

def setRootVal(root, newVal): 
    root[0] = newVal 

def getLeftChild(root): 
    return root[1] 

def getRightChild(root): 
    return root[2] 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
r = BinaryTree(3)
insertLeft(r,4)
print(r)
insertLeft(r,5)
print(r)
insertRight(r,6)
print(r)
l = getLeftChild(r)
print(l)
setRootVal(l,9)
print(r)
insertLeft(l,11)
print(r)
print(getRightChild(getRightChild(r)))
[3, [4, [], []], []]
[3, [5, [4, [], []], []], []]
[3, [5, [4, [], []], []], [6, [], []]]
[5, [4, [], []], []]
[3, [9, [4, [], []], []], [6, [], []]]
[3, [9, [11, [4, [], []], []], []], [6, [], []]]
[]

节点链接表示树：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class BinaryTree: 
    def __init__(self, rootObj): 
        self.key = rootObj 
        self.leftChild = None 
        self.rightChild = None
    def insertLeft(self, newNode): 
        if self.leftChild == None: 
            self.leftChild = BinaryTree(newNode) 
        else: 
            t = BinaryTree(newNode) 
            t.left = self.leftChild 
            self.leftChild = t 
    def insertRight(self, newNode): 
        if self.rightChild == None: 
            self.rightChild = BinaryTree(newNode) 
        else: 
            t = BinaryTree(newNode) 
            t.right = self.rightChild 
            self.rightChild = t
    def getRightChild(self): 
        return self.rightChild 
    def getLeftChild(self): 
        return self.leftChild 
    def setRootVal(self, obj): 
        self.key = obj 
    def getRootVal(self): 
        return self.key
1
2
3
4
5
6
7
r = BinaryTree('a')
print(r.getRootVal())
r.insertLeft('b')
print(r.getLeftChild().getRootVal())
r.insertRight('c')
r.getRightChild().setRootVal('hello')
print(r.getRightChild().getRootVal())
a
b
hello

可以将表达式表示为树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def buildParseTree(fpexp): 
    # fplist = fpexp.split()
    fplist = list(fpexp)
    pStack = Stack() 
    eTree = BinaryTree('') 
    pStack.push(eTree) 
    currentTree = eTree 
    for i in fplist: 
        if i == '(': 
            currentTree.insertLeft('') 
            pStack.push(currentTree) 
            currentTree = currentTree.getLeftChild() 
        elif i not in '+-*/)': 
            currentTree.setRootVal(eval(i)) 
            parent = pStack.pop() 
            currentTree = parent 
        elif i in '+-*/': 
            currentTree.setRootVal(i) 
            currentTree.insertRight('') 
            pStack.push(currentTree) 
            currentTree = currentTree.getRightChild() 
        elif i == ')': 
            currentTree = pStack.pop() 
        else: 
            raise ValueError("Unknown Operator: " + i) 
    return eTree 
1
buildParseTree('((3+5)+(5*6))')
<__main__.BinaryTree at 0x23456a3b4f0>
1
2
3
4
5
6
7
8
9
10
11
import operator
def evaluate(parseTree): 
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv} 
    leftC = parseTree.getLeftChild() 
    rightC = parseTree.getRightChild() 

    if leftC and rightC: 
        fn = opers[parseTree.getRootVal()] 
        return fn(evaluate(leftC), evaluate(rightC)) 
    else: 
        return parseTree.getRootVal() 
1
evaluate(buildParseTree('((3+5)+(5*6))'))
38
1
tree = buildParseTree('((3+5)+(5*6))')
1
tree.getLeftChild().getLeftChild().getRootVal()
3

树的遍历：

前序遍历
中序遍历
后续遍历

1
2
3
4
5
def preorder(tree): 
    if tree: 
        print(tree.getRootVal()) 
        preorder(tree.getLeftChild()) 
        preorder(tree.getRightChild())
1
2
3
4
5
def postorder(tree): 
    if tree != None: 
        postorder(tree.getLeftChild()) 
        postorder(tree.getRightChild()) 
        print(tree.getRootVal()) 
1
2
3
4
5
def inorder(tree): 
    if tree != None: 
        inorder(tree.getLeftChild()) 
        print(tree.getRootVal()) 
        inorder(tree.getRightChild())

也可以写入binary tree class里

1
2
3
4
5
6
def preorder(self): 
    print(self.key) 
    if self.leftChild: 
        self.left.preorder() 
    if self.rightChild: 
        self.right.preorder()

优先队列（vip放在队首）

按优先级排队： 二叉堆（能够将优先队列的入队和出队复杂度都保持在O（logn））
完全二叉树保证平衡：如果节点的下标为p，那么左子节点下标为2p，右子节点下标为2p-1，父节点下标为p//2

内置库实现优先队列的三种方式

例题： LeetCode692

注：第三种方法定义了如何比较item的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
def test_buildin_PriorityQueue():  # python3
    """
    测试内置的 PriorityQueue
    https://pythonguides.com/priority-queue-in-python/
    """
    from queue import PriorityQueue
    q = PriorityQueue()
    q.put((10, 'Red balls'))
    q.put((8, 'Pink balls'))
    q.put((5, 'White balls'))
    q.put((4, 'Green balls'))
    while not q.empty():
        item = q.get()
        print(item)


def test_buildin_heapq_as_PriorityQueue():
    """
    测试使用 heapq 实现优先级队列，保存一个 tuple 比较元素(tuple第一个元素是优先级)
    实际上是利用了元组tuple比较从第一个开始比较的性质
    """
    import heapq
    s_roll = []
    heapq.heappush(s_roll, (4, "Tom"))
    heapq.heappush(s_roll, (1, "Aruhi"))
    heapq.heappush(s_roll, (3, "Dyson"))
    heapq.heappush(s_roll, (2, "Bob"))
    while s_roll:
        deque_r = heapq.heappop(s_roll)
        print(deque_r)


# python3 没有了 __cmp__ 魔法函数 https://stackoverflow.com/questions/8276983/why-cant-i-use-the-method-cmp-in-python-3-as-for-python-2
class Item:
    def __init__(self, key, weight):
        self.key, self.weight = key, weight

    def __lt__(self, other): # heapq 源码实现只用了 小于 比较，这里定义了就可以 push 一个 item 类
        return self.weight < other.weight

#   def __eq__(self, other): # 这个可以省略，只要定义了 __lt__ 魔法函数就可以了
#       return self.weight == other.weight
#
#   def __str__(self):
#       return '{}:{}'.format(self.key,self.weight)

# Item.__lt__ = lambda self, other: self.weight < other.weight # 对于已有的类，直接加一句就可以实现作为 heap item 了

def test_heap_item():
    """
    测试使用 Item 类实现优先级队列，因为 heapq 内置使用的是小于运算法，
    重写魔术 < 比较方法即可实现
    """
    import heapq
    pq = []
    heapq.heappush(pq, Item('c', 3))
    heapq.heappush(pq, Item('a', 1))
    heapq.heappush(pq, Item('b', 2))
    while pq:
        print(heapq.heappop(pq))

堆次序

任何一个节点x，其父节点p中的key均小（或大于）于x中的key，根节点的key最小（或最小）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class BinHeap:
    def __init__(self): 
        self.heapList = [0] 
        self.currentSize = 0
    def percUp(self, i): 
        # 将新数据上浮到合适的位置（大小），以便执行插入操作
        while i // 2 > 0: 
            if self.heapList[i] < self.heapList[i // 2]: 
                self.heapList[i // 2], self.heapList[i] = self.heapList[i], self.heapList[i // 2]
            i = i // 2
    def insert(self, k): 
        self.heapList.append(k) 
        self.currentSize = self.currentSize + 1 
        self.percUp(self.currentSize)
    def percDown(self, i): 
        # 删除最小节点时，先将最后一个节点放到删除节点处，再下沉
        while (i * 2) <= self.currentSize: 
            mc = self.minChild(i) 
            if self.heapList[i] > self.heapList[mc]: 
                self.heapList[i], self.heapList[mc] = self.heapList[mc], self.heapList[i]
            i = mc 
    def minChild(self, i): 
        if i * 2 + 1 > self.currentSize: 
            return i * 2 
        else: 
            if self.heapList[i*2] < self.heapList[i*2+1]: 
                return i * 2 
            else: 
                return i * 2 + 1
    def delMin(self): 
        retval = self.heapList[1] 
        self.heapList[1] = self.heapList[self.currentSize] 
        self.currentSize = self.currentSize - 1 
        self.heapList.pop() 
        self.percDown(1) 
        return retval 
    def buildHeap(self, alist): 
        # 复杂度为O 1
        i = len(alist) // 2
        self.currentSize = len(alist) 
        self.heapList = [0] + alist[:] 
        while (i > 0): 
            self.percDown(i) 
            i = i - 1

堆排序复杂度O（nlogn）
最大和最后一个叶子交换顺序后调整需要O(logn)， 总共n个节点。
注：建堆的复杂度为O(n)

堆

具有堆次序的完全二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def heapify(arr, n, i): 
    largest = i  
    l = 2 * i + 1     # left = 2*i + 1 
    r = 2 * i + 2     # right = 2*i + 2 
  
    if l < n and arr[i] < arr[l]: 
        largest = l 
  
    if r < n and arr[largest] < arr[r]: 
        largest = r 
  
    if largest != i: 
        arr[i],arr[largest] = arr[largest],arr[i]  # 交换
  
        heapify(arr, n, largest) 
  
def heapSort(arr): 
    n = len(arr) 
  
    # Build a maxheap. 
    for i in range(n, -1, -1): 
        heapify(arr, n, i) 
  
    # 一个个交换元素
    for i in range(n-1, 0, -1): 
        arr[i], arr[0] = arr[0], arr[i]   # 交换
        heapify(arr, i, 0) 
  
arr = [ 12, 11, 13, 5, 6, 7] 
heapSort(arr) 
n = len(arr) 
print ("排序后") 
for i in range(n): 
    print ("%d" %arr[i]),
排序后
5
6
7
11
12
13

内置库实现最大堆

python自带的heapq实现了最小堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 方法1:封装一个 max heap 类
import heapq
class MaxHeap:
    """
    https://stackoverflow.com/questions/2501457/what-do-i-use-for-a-max-heap-implementation-in-python
    """
    def __init__(self, capacity):
        self.capacity = capacity
        self.minheap = []

    def push(self, val):
        heapq.heappush(self.minheap, -val)  # push取反后的数字, 1 -> -1

    def pop(self):
        val = heapq.heappop(self.minheap)
        return -val # 拿出来的数字再取反

    def max(self):
        return -self.minheap[0] # min-heap 的数组最小值是 m[0]，最大值取反

# 方法2: 重新定几个新的 max-heap 方法
import heapq
def maxheappush(h, item):
    return heapq.heappush(h, -item)

def maxheappop(h):
    return -heapq.heappop(h)

def maxheapval(h):
    return -h[0]

二叉查找树

比父节点小的key都出现在左子树，比父节点大的出现在右子树

ADT Map（抽象数据类型映射）之前已经有两种实现方法：1.有序表+二分搜索。2. hash表。下面用二叉查找树实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class TreeNode: 
    def __init__(self, key, val, left=None, right=None, 
        parent=None): 
        self.key = key 
        self.payload = val 
        self.leftChild = left 
        self.rightChild = right 
        self.parent = parent 
    def hasLeftChild(self): 
        return self.leftChild 
    def hasRightChild(self): 
        return self.rightChild 
    def isLeftChild(self): 
        return self.parent and self.parent.leftChild == self
    def isRightChild(self): 
        return self.parent and self.parent.rightChild == self 
    def isRoot(self): 
        return not self.parent 
    def isLeaf(self): 
        return not (self.rightChild or self.leftChild) 
    def hasAnyChildren(self): 
        return self.rightChild or self.leftChild 
    def hasBothChildren(self): 
        return self.rightChild and self.leftChild 
    def replaceNodeData(self, key, value, lc, rc): 
        self.key = key 
        self.payload = value 
        self.leftChild = lc 
        self.rightChild = rc 
        if self.hasLeftChild(): 
            self.leftChild.parent = self 
        if self.hasRightChild(): 
            self.rightChild.parent = self
    def __iter__(self): 
        if self: 
            if self.hasLeftChild(): 
                for elem in self.leftChild: 
                    yield elem 
            yield self.key 
            if self.hasRightChild(): 
                for elem in self.rightChild: 
                    yield elem
    def findSuccessor(self): 
        succ = None 
        if self.hasRightChild(): 
            succ = self.rightChild.findMin() 
        else: 
            if self.parent: 
                if self.isLeftChild(): 
                    succ = self.parent 
                else: 
                    self.parent.rightChild = None 
                    succ = self.parent.findSuccessor() 
                    self.parent.rightChild = self 
        return succ
    def findMin(self): 
        current = self 
        while current.hasLeftChild(): 
            current = current.leftChild 
        return current
    def spliceOut(self): 
        if self.isLeaf(): 
            if self.isLeftChild(): 
                self.parent.leftChild = None 
            else: 
                self.parent.rightChild = None 
        elif self.hasAnyChildren(): 
            if self.hasLeftChild(): 
                if self.isLeftChild(): 
                    self.parent.leftChild = self.leftChild 
                else: 
                    self.parent.rightChild = self.leftChild 
                self.leftChild.parent = self.parent 
            else: 
                if self.isLeftChild(): 
                    self.parent.leftChild = self.rightChild 
                else: 
                    self.parent.rightChild = self.rightChild 
                self.rightChild.parent = self.parent
    

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
class BinarySearchTree: 
    def __init__(self): 
        self.root = None 
        self.size = 0 
    def length(self): 
        return self.size 
    def __len__(self): 
        return self.size 
    def __iter__(self): 
        # for 循环
        return self.root.__iter__()
    def put(self, key, val): 
        if self.root: 
            self._put(key, val, self.root) 
        else: 
            self.root = TreeNode(key, val) 
            self.size = self.size + 1 
    def _put(self, key, val, currentNode): 
        if key < currentNode.key: 
            if currentNode.hasLeftChild(): 
                self._put(key, val, currentNode.leftChild) 
            else: 
                currentNode.leftChild = TreeNode(key, val, parent=currentNode) 
        else: 
            if currentNode.hasRightChild(): 
                self._put(key, val, currentNode.rightChild) 
            else: 
                currentNode.rightChild = TreeNode(key, val, parent=currentNode)
    def __setitem__(self, k, v): 
        # m[k] = v
        self.put(k, v)
    def get(self, key): 
        if self.root: 
            res = self._get(key, self.root) 
            if res: 
                return res.payload 
            else: 
                return None 
        else: 
            return None 
    def _get(self, key, currentNode): 
        if not currentNode: 
            return None 
        elif currentNode.key == key: 
            return currentNode 
        elif key < currentNode.key: 
            return self._get(key, currentNode.leftChild)
        else: 
            return self._get(key, currentNode.rightChild) 
    def __getitem__(self, key): 
        return self.get(key)
    def __contains__(self, key): 
        # k in m
        if self._get(key, self.root): 
            return True 
        else: 
            return False
    def delete(self, key): 
        if self.size > 1: 
            nodeToRemove = self._get(key, self.root) 
            if nodeToRemove: 
                self.remove(nodeToRemove) 
                self.size = self.size - 1 
            else: 
                raise KeyError('Error, key not in tree') 
        elif self.size == 1 and self.root.key == key: 
            self.root = None 
            self.size = self.size - 1 
        else: 
            raise KeyError('Error, key not in tree') 
    def __delitem__(self, key): 
        self.delete(key)
    
    
    
    def remove(self, currentNode): 
        if currentNode.isLeaf(): # 叶子节点
            if currentNode == currentNode.parent.leftChild: 
                currentNode.parent.leftChild = None 
            else: 
                currentNode.parent.rightChild = None 
        elif currentNode.hasBothChildren(): # 内部 
            succ = currentNode.findSuccessor() 
            succ.spliceOut() 
            currentNode.key = succ.key 
            currentNode.payload = succ.payload 
        else: # 只有一个子节点
            if currentNode.hasLeftChild(): 
                if currentNode.isLeftChild(): 
                    currentNode.leftChild.parent = currentNode.parent 
                    currentNode.parent.leftChild = currentNode.leftChild 
                elif currentNode.isRightChild(): 
                    currentNode.leftChild.parent = currentNode.parent 
                    currentNode.parent.rightChild = currentNode.leftChild 
                else: 
                    currentNode.replaceNodeData(currentNode.leftChild.key, 
                                            currentNode.leftChild.payload, 
                                            currentNode.leftChild.leftChild, 
                                            currentNode.leftChild.rightChild) 
            else: 
                if currentNode.isLeftChild(): 
                    currentNode.rightChild.parent = currentNode.parent 
                    currentNode.parent.leftChild = currentNode.rightChild 
                elif currentNode.isRightChild(): 
                    currentNode.rightChild.parent = currentNode.parent 
                    currentNode.parent.rightChild = currentNode.rightChild 
                else: 
                    currentNode.replaceNodeData(currentNode.rightChild.key, 
                                            currentNode.rightChild.payload, 
                                            currentNode.rightChild.leftChild, 
                                            currentNode.rightChild.rightChild)


如果root是中位数，那就是比较平衡的，插入顺序影响很大。

平衡二叉查找树： AVL树

key插入的时候一直保持平衡，避免上述情况
搜索时间复杂度为O（logn）
左节点+1，右节点-1
AVL树旋转的过程是核心

具体解析可以参见：《python数据结构与算法分析》第六章-平衡二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
class BinarySearchTree: 
    def __init__(self): 
        self.root = None 
        self.size = 0 
    def length(self): 
        return self.size 
    def __len__(self): 
        return self.size 
    def __iter__(self): 
        # for 循环
        return self.root.__iter__()
    def put(self, key, val): 
        if self.root: 
            self._put(key, val, self.root) 
        else: 
            self.root = TreeNode(key, val) 
            self.size = self.size + 1 
    # def _put(self, key, val, currentNode): 
    #     if key < currentNode.key: 
    #         if currentNode.hasLeftChild(): 
    #             self._put(key, val, currentNode.leftChild) 
    #         else: 
    #             currentNode.leftChild = TreeNode(key, val, parent=currentNode) 
    #     else: 
    #         if currentNode.hasRightChild(): 
    #             self._put(key, val, currentNode.rightChild) 
    #         else: 
    #             currentNode.rightChild = TreeNode(key, val, parent=currentNode)
    def __setitem__(self, k, v): 
        # m[k] = v
        self.put(k, v)
    def get(self, key): 
        if self.root: 
            res = self._get(key, self.root) 
            if res: 
                return res.payload 
            else: 
                return None 
        else: 
            return None 
    def _get(self, key, currentNode): 
        if not currentNode: 
            return None 
        elif currentNode.key == key: 
            return currentNode 
        elif key < currentNode.key: 
            return self._get(key, currentNode.leftChild)
        else: 
            return self._get(key, currentNode.rightChild) 
    def __getitem__(self, key): 
        return self.get(key)
    def __contains__(self, key): 
        # k in m
        if self._get(key, self.root): 
            return True 
        else: 
            return False
    def delete(self, key): 
        if self.size > 1: 
            nodeToRemove = self._get(key, self.root) 
            if nodeToRemove: 
                self.remove(nodeToRemove) 
                self.size = self.size - 1 
            else: 
                raise KeyError('Error, key not in tree') 
        elif self.size == 1 and self.root.key == key: 
            self.root = None 
            self.size = self.size - 1 
        else: 
            raise KeyError('Error, key not in tree') 
    def __delitem__(self, key): 
        self.delete(key)
    
    
    
    def remove(self, currentNode): 
        if currentNode.isLeaf(): # 叶子节点
            if currentNode == currentNode.parent.leftChild: 
                currentNode.parent.leftChild = None 
            else: 
                currentNode.parent.rightChild = None 
        elif currentNode.hasBothChildren(): # 内部 
            succ = currentNode.findSuccessor() 
            succ.spliceOut() 
            currentNode.key = succ.key 
            currentNode.payload = succ.payload 
        else: # 只有一个子节点
            if currentNode.hasLeftChild(): 
                if currentNode.isLeftChild(): 
                    currentNode.leftChild.parent = currentNode.parent 
                    currentNode.parent.leftChild = currentNode.leftChild 
                elif currentNode.isRightChild(): 
                    currentNode.leftChild.parent = currentNode.parent 
                    currentNode.parent.rightChild = currentNode.leftChild 
                else: 
                    currentNode.replaceNodeData(currentNode.leftChild.key, 
                                            currentNode.leftChild.payload, 
                                            currentNode.leftChild.leftChild, 
                                            currentNode.leftChild.rightChild) 
            else: 
                if currentNode.isLeftChild(): 
                    currentNode.rightChild.parent = currentNode.parent 
                    currentNode.parent.leftChild = currentNode.rightChild 
                elif currentNode.isRightChild(): 
                    currentNode.rightChild.parent = currentNode.parent 
                    currentNode.parent.rightChild = currentNode.rightChild 
                else: 
                    currentNode.replaceNodeData(currentNode.rightChild.key, 
                                            currentNode.rightChild.payload, 
                                            currentNode.rightChild.leftChild, 
                                            currentNode.rightChild.rightChild)
    def _put(self, key, val, currentNode): 
        if key < currentNode.key: 
            if currentNode.hasLeftChild(): 
                self._put(key, val, currentNode.leftChild) 
            else: 
                currentNode.leftChild = TreeNode(key, val, parent=currentNode) 
                self.updateBalance(currentNode.leftChild) 
        else: 
            if currentNode.hasRightChild(): 
                self._put(key, val, currentNode.rightChild) 
            else: 
                currentNode.rightChild = TreeNode(key, val, parent=currentNode) 
                self.updateBalance(currentNode.rightChild) 
    def updateBalance(self, node): 
        if node.balanceFactor > 1 or node.balanceFactor < -1: 
            self.rebalance(node) 
            return 
        if node.parent != None: 
            if node.isLeftChild(): 
                node.parent.balanceFactor += 1 
            elif node.isRightChild(): 
                node.parent.balanceFactor -= 1 
            if node.parent.balanceFactor != 0: 
                self.updateBalance(node.parent)
    def rotateLeft(self, rotRoot): 
        newRoot = rotRoot.rightChild 
        rotRoot.rightChild = newRoot.leftChild 
        if newRoot.leftChild != None: 
            newRoot.leftChild.parent = rotRoot 
        newRoot.parent = rotRoot.parent 
        if rotRoot.isRoot(): 
            self.root = newRoot 
        else: 
            if rotRoot.isLeftChild(): 
                rotRoot.parent.leftChild = newRoot 
            else: 
                rotRoot.parent.rightChild = newRoot 
        newRoot.leftChild = rotRoot 
        rotRoot.parent = newRoot 
        rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor, 0) 
        newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0)
    def rebalance(self, node): 
        if node.balanceFactor < 0: 
            if node.rightChild.balanceFactor > 0: 
                self.rotateRight(node.rightChild) 
                self.rotateLeft(node) 
            else: 
                self.rotateLeft(node) 
        elif node.balanceFactor > 0: 
            if node.leftChild.balanceFactor < 0: 
                self.rotateLeft(node.leftChild) 
                self.rotateRight(node) 
            else: 
                self.rotateRight(node)


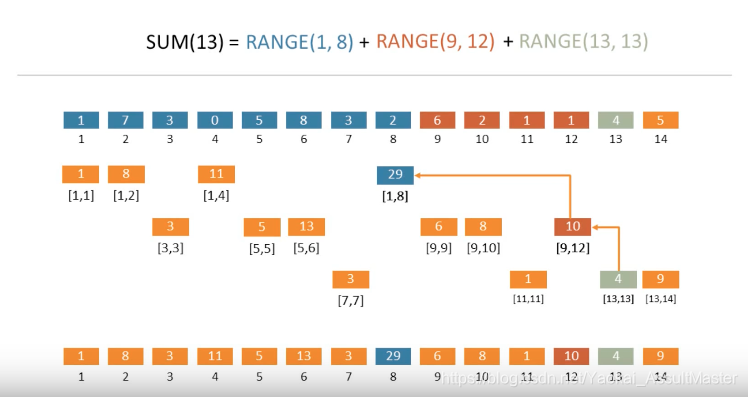
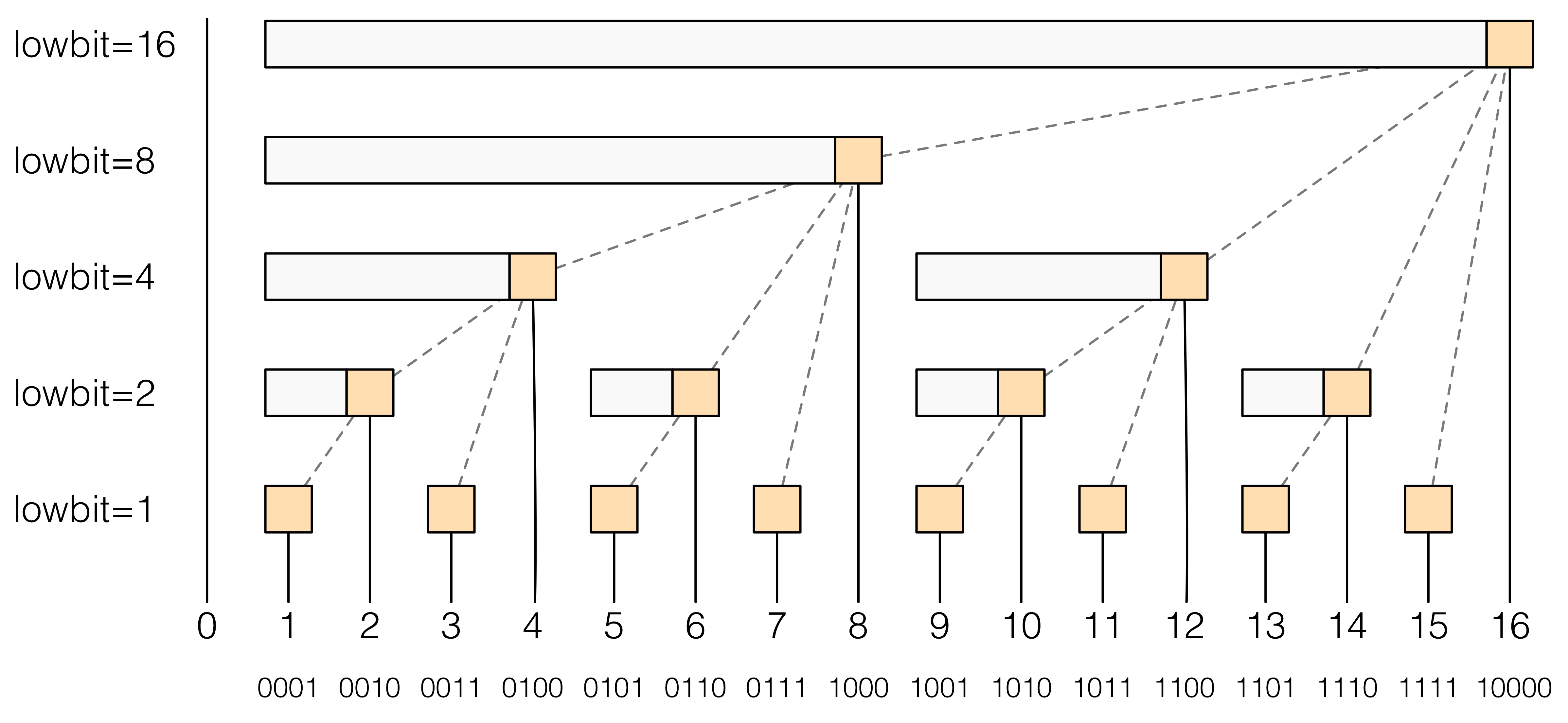
树状数组

Compute sum by going up and left based on Binary Indexed Treebinary_index_tree.png

Binary Indexed Tree：存储数字，可以高效更新和求前缀和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class NumArray:
    def __init__(self, nums: List[int]):
        self.nums = nums
        self.tree = [0] * (len(nums) + 1)
        for i, num in enumerate(nums, 1):
            self.add(i, num)

    def add(self, index: int, val: int):
        while index < len(self.tree):
            self.tree[index] += val
            index += index & -index

    def prefixSum(self, index) -> int:
        s = 0
        while index:
            s += self.tree[index]
            index &= index - 1
        return s

    def update(self, index: int, val: int) -> None:
        self.add(index + 1, val - self.nums[index])
        self.nums[index] = val

    def sumRange(self, left: int, right: int) -> int:
        return self.prefixSum(right + 1) - self.prefixSum(left)

树状数组 & 线段树 详细解释

关键在于理解:

  • index & (index - 1)是求前图左上角的index值
  • add中index += index $ -index是求下一个包含该值的index
  • 动画解释

LeetCode 307

LeetCode 315

线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
'''ST：Segment Tree 线段树'''
class NumArray:
    
    def __init__(self, nums: List[int]):
        n = len(nums)
        self.n = n
        self.tree = [0]*n + nums    # 线段树ST长度为2n
        for i in range(n-1, 0, -1): # [1, n-1] 倒序添加，子节点之和
            # ST[2i]和ST[2i+1]分别为ST[i]的左右子节点
            self.tree[i] = self.tree[2*i] + self.tree[2*i+1]

    def update(self, index: int, val: int) -> None:
        i = index + self.n              # nums下标转换到ST下标
        delta = val-self.tree[i]        # 变更值
        while i:                        # 自下而上进行更新
            self.tree[i] += delta
            i //= 2

    def sumRange(self, left: int, right: int) -> int:
        i, j = left+self.n, right+self.n    # nums下标转换到ST下标
        summ = 0
        while i<=j:
            if i%2 == 1:    # ST[i]是右子节点
                summ += self.tree[i]    # 计入ST[i]，并i+1（转向下一个区间）
                i += 1
            if j%2 == 0:    # ST[j]是左子节点
                summ += self.tree[j]    # 计入ST[j]，并j-1（转向上一个区间）
                j -= 1
            i, j = i//2, j//2
        return summ


图

顶点vertex，边edge
权重：给边赋权
G = (V, E) 有向图，无向图
有向无圈图：directed acyclic graph:DAG

ADT Graph两种实现方式：

  • 邻接矩阵adjacency matrix
    • 无权边标注为1或0，有权边标注为相应权重
  • 邻接表adjacency list
    • 类似字典
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Vertex: 
    def __init__(self, key): 
        self.id = key 
        self.connectedTo = {} 
    def addNeighbor(self, nbr, weight=0): 
        self.connectedTo[nbr] = weight 
    def __str__(self): 
        return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
    def getConnections(self): 
        return self.connectedTo.keys() 
    def getId(self): 
        return self.id 
    def getWeight(self, nbr): 
        return self.connectedTo[nbr]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Graph: 
    def __init__(self): 
        self.vertList = {} 
        self.numVertices = 0 

    def addVertex(self, key): 
        self.numVertices = self.numVertices + 1 
        newVertex = Vertex(key) 
        self.vertList[key] = newVertex 
        return newVertex 

    def getVertex(self, n): 
        if n in self.vertList: 
            return self.vertList[n] 
        else: 
            return None 

    def __contains__(self, n): 
        return n in self.vertList 

    def addEdge(self, f, t, cost=0): 
        if f not in self.vertList: 
            nv = self.addVertex(f) 
        if t not in self.vertList: 
            nv = self.addVertex(t) 
        self.vertList[f].addNeighbor(self.vertList[t], cost) 

    def getVertices(self): 
        return self.vertList.keys() 

    def __iter__(self): 
        return iter(self.vertList.values())

并查集

1
2
3
4
5
6
7
8
9
10
11
12
class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))

    def union(self, index1: int, index2: int):
        self.parent[self.find(index2)] = self.find(index1)

    def find(self, index: int) -> int:
        if self.parent[index] != index:
            self.parent[index] = self.find(self.parent[index])
        return self.parent[index]

1
2
3
4
5
6
7
8
9
f = {}
        def union(x,y):
            f[find(x)] = find(y)
            
        def find(x):
            f.setdefault(x,x)
            if f[x]!=x:
                f[x] = find(f[x])
            return f[x]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def find(i):
    if parent[i] == i:
        return i
    else:
        parent[i] = find(parent[i])
        return parent[i]
def union(i,j):
    i_parent = find(i)
    j_parent = find(j)
    parent[i_parent] = j_parent
    
parent = []
for i in range(n):
    parent[i] = i

广度优先搜索:O(V+E)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from pythonds.graphs import Graph, Vertex 
from pythonds.basic import Queue 
def bfs(g, start): 
    start.setDistance(0) 
    start.setPred(None) 
    vertQueue = Queue() 
    vertQueue.enqueue(start) 
    while (vertQueue.size() > 0): 
        currentVert = vertQueue.dequeue() 
        for nbr in currentVert.getConnections(): 
            if (nbr.getColor() == 'white'): 
                nbr.setColor('gray') 
                nbr.setDistance(currentVert.getDistance() + 1) 
                nbr.setPred(currentVert) 
                vertQueue.enqueue(nbr) 
        currentVert.setColor('black')
1
2
3
4
5
6
7
8
9
# 回溯BFS
def traverse(y): 
    x = y 
    while (x.getPred()): 
        print(x.getId()) 
        x = x.getPred() 
        print(x.getId()) 

# traverse(g.getVertex('sage'))

深度优先搜索：O（V+E）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from pythonds.graphs import Graph 
class DFSGraph(Graph): 
    def __init__(self): 
        super(). __init__() 
        self.time = 0 
        
    def dfs(self): 
        for aVertex in self: 
            aVertex.setColor('white') 
            aVertex.setPred(-1) 
        for aVertex in self: 
            if aVertex.getColor() == 'white': 
                self.dfsvisit(aVertex) 

    def dfsvisit(self, startVertex): 
        startVertex.setColor('gray') 
        self.time += 1 
        startVertex.setDiscovery(self.time) 
        for nextVertex in startVertex.getConnections(): 
            if nextVertex.getColor() == 'white': 
                nextVertex.setPred(startVertex) 
                self.dfsvisit(nextVertex) 
        startVertex.setColor('black') 
        self.time += 1 
        startVertex.setFinish(self.time)

图的应用：拓扑排序

拓扑排序根据有向无环图生成一个包含所有顶点的线性序列，使得如果图 G 中有一条边为(v, w)，那么顶点 v 排在顶点 w 之前。在很多应用中，有向无环图被用于表明事件优先级。

图的应用：强连通分支

C中的任意两个顶点之间都有路径来回，这样的最大的子集就是强连通分支
强连通分支的矩阵和转置矩阵相同

  • kosaraju算法: 先用dfs得到每个顶点结束时间，然后按照结束时间最大的作为顶点，在转置图中用dfs，这样得到的所有顶点链接树就是强连通分支
  • Tarjan算法
  • Gabow算法（性能最高）

图的应用：最短路径

  • Dijkstra算法：（只能处理大于0权重的图）O((V+E)logV)
    • 利用优先队列：所有顶点建堆，然后出队优先点，更新邻接点的权值，并在优先队列中重排，直到优先队列中没有点
    • 距离向量路由算法
1
2
3
4
5
6
7
8
9
10
11
12
13
from pythonds.graphs import PriorityQueue, Graph, Vertex 
def dijkstra(aGraph, start): 
    pq = PriorityQueue() 
    start.setDistance(0) 
    pq.buildHeap([(v.getDistance(), v) for v in aGraph]) 
    while not pq.isEmpty(): 
        currentVert = pq.delMin() 
        for nextVert in currentVert.getConnections(): 
            newDist = currentVert.getDistance() + currentVert.getWeight(nextVert) 
        if newDist < nextVert.getDistance(): 
            nextVert.setDistance(newDist) 
            nextVert.setPred(currentVert) 
            pq.decreaseKey(nextVert, newDist) # O(ElogV)

图的应用：最小生成树(minimum weight spanning tree)

  • 拥有图中所有顶点和最小数量的边（权重和最小）以保持联通的子图（无圈）
  • prim算法（和dijkstra算法相似，只不过要采取贪心策略，加入所有的顶点）

python小技巧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
itertools.combinations(indexlist,2)

enumerate(indexlist)

dummynode = ListNode(-1)

low, high = 0, n-1
while low <= high:
    
collections.deque([])
collections.defaultdict(list)

__lt__()


注意：

lista = listb[:]相当于一次拷贝，与lista = listb是不一样的

Related Posts