Machine Learning Week10
Large Scale Machine Learning
Gradient Descent with Large Datasets
Learning with large datasets
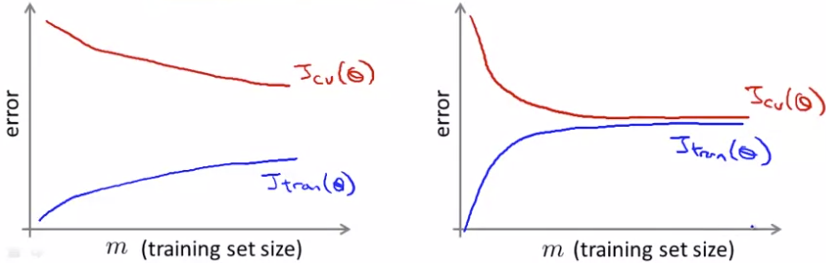
如何知道小m(size of dataset)也能产生很好的结果?绘制learning curve(error关于m的曲线)
左图为high variance,说明增加m有助于结果变好;右图为high bias,说明增加m无助于结果变好
Stochastic gradient descent 随机梯度下降
Batch gradient descent: 前述传统的梯度下降算法。batch意味着每次都要用到所有m个例子
Stochastic gradient descent:每次iteration用1个例子
Randomly shuffle dataset
Repeat:
for i =1,..., m { \(\theta_j=\theta_j-\alpha(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}\) }
Note: 和Batch gradient descent不同的是,无需每一步都要计算全部的training example
并不一定会达到global minimum,最后可能在全局最优附近徘徊。
上述过程重复的次数取决于数据集的大小,一般为10次,若数据集特别大,则1次。
Mini-Batch gradient descent
每次iteration用b(mini-batch size)个例子,常用2-100
第i个例子,直到第i+b-1个例子

只有当have a good vetorized implementation ,mini-batch才能比stochastic表现得更好。(并行运算)
Stochastic gradient descent convergence
收敛性:

更小的学习速率学习曲线更平滑,有可能会得到slightly better结果。(cost关于no. of iteration 的曲线)
增加1000这个数值,会使得曲线更加平滑
如果学习曲线在上升,就要用更小的α
如果学习曲线几乎在一个水平上,那么就需要增加特征等
关于学习速率的选择:
- Learning rate α is typically held constant 在随机梯度下降中
- Can slowly decrease α over time if we want θ to converge.
(例如:\(\alpha=\frac{const1}{iteration
Number+const2}\))
- 但是这里,两个参数的调整tune会很费时间,所以很少采用这种方法
Advanced Topics
### Online Learning
连续的数据流:用户进入离开
\(p(y=1|x;\theta)\)其中x表示价格,可以用logistic regression或者神经网络
这里考虑逻辑回归:
Repeat forever {
Get (x,y) corresponding to user.
Update θ using (x,y):
\(\theta_j:=\theta_j-\alpha(h_{\theta}(x)-y)x_j\) (j=0, ..., n)
}
这个算法可以用于学习用户喜好
- Choosing special offers to show user
- Customized selection of news articles
- product recommendation/search
Map reduce and data parallelism
Map reduce 可以处理更多数据。思想来自于Jeffrey Dean和Sanjay Ghemawat。summation over the training set。即并行处理
- 神经网络也同样可以并行计算前向和后向propagation
- 有时只需要向量化实现算法,不需要多核并行
- Hadoop是开源map reduce
- 由于并行的latency,速度会少于N倍 的单核心