Machine Learning Week08

Posted on Edited on In Views: Symbols count in article: 3.8k Reading time ≈ 3 mins.

Unsupervised learning 无监督学习

Clustering 聚类

无监督学习是不给分类标签y

1. 应用：

  • 对消费者市场划分
  • 社交网络分析
  • 管理计算机
  • 获取星系信息

2. K-means algorithm K均值算法

  • 随机选择两个点作为聚类中心(分两类)，然后进行下面两步

    • 簇分配，遍历每个点，和哪个cluster centroid更近
    • 移动聚类中心到上面分配的簇的均值

  • Input:

    • K - number of clusters
    • training set

  • algorithm

    1
    2
    3
    4
    5
    6
     repeat{
    	for i=1 to m
    		c_i := index (from 1 to K) of cluster centroid closest to x_i
        for k=1 to K
        	u_k := average (mean) of points assigned to cluster k
    }

  • 如果有中心没有被分配到任何点，可以删去这个分类，也可以reinitialize the cluster centroid

3. K-means for non-sperated clusters

  • 根据身高体重分类T恤大小

4. Optimization Objective

  • \[ \begin{array}{l} J\left(c^{(1)}, \ldots, c^{(m)}, \mu_{1}, \ldots, \mu_{K}\right)=\frac{1}{m} \sum_{i=1}\left\|x^{(i)}-\mu_{c^{(i)}}\right\|^{2} \\ \min _{c^{(1)}, \ldots, c^{(m)},\mu_{1}, \ldots, \mu_{K}} J\left(c^{(1)}, \ldots, c^{(m)}, \mu_{1}, \ldots, \mu_{K}\right) \end{array} \]

  • also called distortion of K-means algorithm

  • cost function 关于iteration的曲线

5. Random Initialization

随机初始化聚类中心

随机选k个个例本身，作为中心，但是容易陷入Local optima。解决方案：多次随机，选择cost function最小的

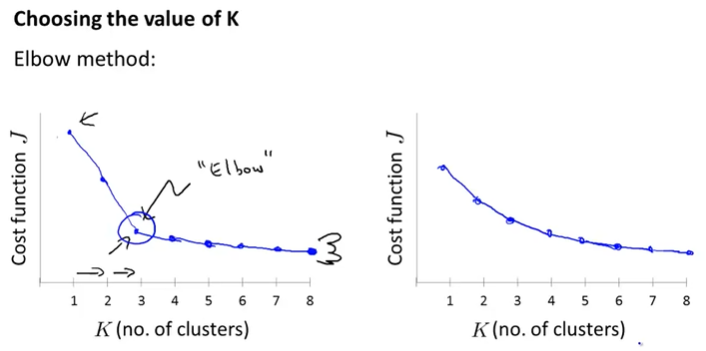
6. Choosing the Number of Clusters

Elbow Method:

绘制J关于K的曲线，找到“Elbow”的节点，作为分类个数

image-20210331185002558

用途之一：later/downstream purpose

Motivation

1. Data Compression ---- Dimensionality Reduction降维

压缩数据，减少内存占用加快运算

2. Data Visualization

降维可以便于数据可视化

Principal Component Analysis主成分分析

1. Problem formulation

PCA：To find a surface onto which to project the data so as to minimize the the projection error (线性拟合中就是使得离某条直线的距离最小).

  • 先mean normalization（feature scaling）
  • Reduce from 2-dimension to 1-dimension: Find a direction (a vector \(u_i\in \R^n\)) onto which to project the data so as to minimize the projection error. 该向量的正负没有关系。
  • Reduce from n-dimension to k-dimension: Find k vectors \(u^{(1)}\),\(u^{(2)}\), ... , \(u^{(k)}\) onto which to project the data so as to minimize the projection error.
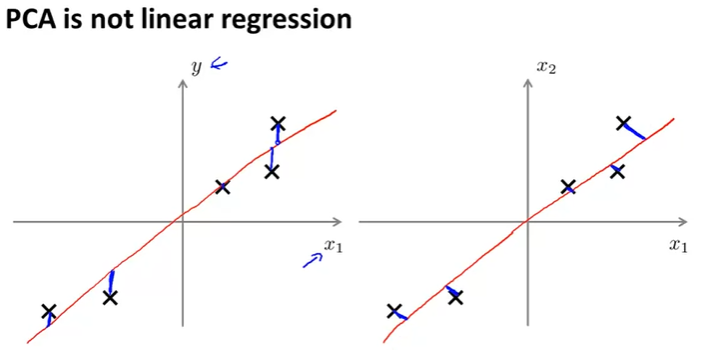
  • 注：PCA is not linear regression。注意看下图区别，线性回归是和预期值的差最小，PCA是到直线距离最小
image-20210331214953585

2. PCA Algorithm

PCA的目标：

  • maximize variance perspective 最大投影方差
  • minimize error perspective 最小重构代价

Step1: mean normalization. 根据数据(有不同的scales)，可能还需要feature scaling。均值归一化是特征缩放的一种方法。（除以标准差）

image-20210331224012613

Step2: Reduce data from n-dimensions to k-dimensions：

  • Compute "covariance matrix": \(\Sigma = \frac{1}{m}\sum_{i=1}^{n}{(x^{(i)})(x^{(i)})^T}\)，xi是n*1的列向量，symmetric positive definite

  • Compute "eigenvectors" of matrix \(\Sigma\): [U, S, V] = svd(Sigma) ;或者 eig(Sigma)

    svd: Singular value decomposition 奇异值分解

    其中U是我们需要的， 列向量为各个特征向量，压缩到k个向量只需要取前k个列向量（对称矩阵的特征向量是正交的）

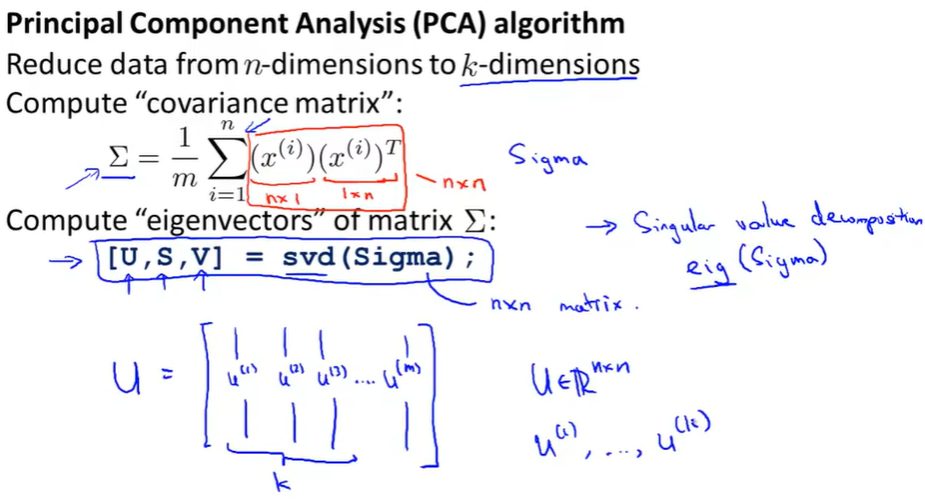
image-20210401221235384
image-20210401222501123

注：PCA算法中，没有x0=1这一项imgimg

疑问：

  1. 为什么不直接用X进行SVD，而要算协方差的SVD？

    Answer：协方差的U和X的V是相等的，其实都可以

    理解：\(X=U'S'V'^T\), \(X^TX=USV^T\)，现要说明 \(V'=U\), 只需要 \(X^TX=V'S'^2V'^T=USV^T\)，所以 \(V'=U\)。

  2. 为什么要取协方差矩阵SVD后的左奇异矩阵来压缩特征维度？

    首先易证一个SPD矩阵通过SVD得到的U和V是相等的。

    其次，通常我们用XV=YU来表示坐标变换。

    \(\Sigma = X^TX\)，又有 \(\Sigma = USV^T\)，可以得到 \(\Sigma V = US\)，这里实际上是将covariance矩阵变化为对角线矩阵，即互不相关（其中U=V，即U为协方差矩阵的特征向量，S为其特征值）。那么这时，我们令XI=UZ，I是X坐标系下的正交基，即 \(Z=U^TX\)。此时Z的协方差 \(Z^TZ=\Sigma\)。

Applying PCA

Reconstruction from compressed representation

\[ z=U_{reduce}^Tx \]

可以得到： \[ x_{approx}=U_{reduce}z \]

Choosing the number k of principal component

  • Average squared projection error：

\[ \frac{1}{m}\Sigma_{i=1}^m\parallel x^{(i)}-x_{approx}^{(i)}\parallel ^2 \]

  • Tptal variation in the data: \[ \frac{1}{m}\Sigma_{i=1}^m\parallel x^{(i)}\parallel ^2 \]

  • Choose k to be smallest value so that \[ \frac{\frac{1}{m}\Sigma_{i=1}^m\parallel x^{(i)}-x_{approx}^{(i)}\parallel ^2}{\frac{1}{m}\Sigma_{i=1}^m\parallel x^{(i)}\parallel ^2}\le0.01 \] "99% of variance is retained"。这个数值可以根据需求不同更换。

  • 算法：

    SVD函数返回的S矩阵为diagonal matrix。

    For given k: k 递增，使得 \[ 1-\frac{\Sigma_{i=1}^{k}S_{ii}}{\Sigma_{i=1}^{n}S_{ii}}\le0.01 \]

    选择最小的K满足上式。

    根据性质：矩阵特征值之和等于主对角线元素之和，易证(6)式等价于(7)式。

Advice for applying PCA

  1. Supervised learning speedup

    压缩原始训练集数据的维度

    Mapping \(x^{(i)}\rightarrow z^{(i)}\)should be defined by running PCA only on the trainning set. This mapping can be applied as well to the examples \(x_{CV}^{(i)}\) and \(x_{test}^{(i)}\) in the cross validation and test sets.

  2. Compression

    • Reduce memory/disk needed to store data
    • speed up learning algorithm

  3. Visualization

  4. Bad use of PCA: To prevent overfitting

    可能确实可以避免过拟合，但是不是解决过拟合的好方法。正确方法式加正则项(Use regularization instead!)

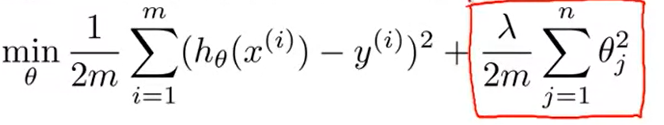
    For example: image-20210403175514854

  5. 正确做法是先不用PCA，在原始数据跑一遍，如果不符合期望，再用PCA

Related Posts