Machine Learning Week06
Deciding What to Try Next
Evaluating a Learning Algorithm
误差大的改进方法:
- 更多数据
- 更少特征集避免过拟合
- 更多特征
- 增加多项式特征
- 减少或增大正则化参数值
评估假设函数Evaluating a Hypothesis
如何判断过拟合?
随机将数据分为两部分,一部分是训练集,一部分是预测集(30%)
学习训练集的参数θ(即最小化训练误差J )
计算测试集误差
线性回归中计算测试集的 J(θ)
逻辑回归中可以用误分类率来计算error:
\(err(h_\theta(x),y)=\begin{cases}1,&if\ h_\theta(x)\ge 0.5,y=0\ or\ if\ h_\theta(x)<0.5, y=1\\0, &otherwise\end{cases}\)
\(Test\ error=\frac{1}{m_{test}}\sum\limits_{i=1}^{m_{test}}err(h_\theta(x_{test}^{(i)},y^{(i)}))\)
模型选择问题:确定对于某组数据最合适的多项式是几次,怎样选用正确的特征来构造学习算法,或者需要正确选择算法中的正则化参数λ
- 将数据分为三段:训练集(60%),交叉验证集(cross validation)(20%),测试集(20%)
- 用不同的多项式模型得到θ,然后计算交叉验证集的误差,看看哪个模型中CV集的误差最小,进而选择那个多项式模型
- 最后计算测试集误差评价模型表现
Bias vs. Variance
分析bias和variance
- 高偏差:欠拟合;高方差:过拟合
- 高偏差:
- \(J_{train}(\theta)\)will be high, the same as \(J_{CV}(\theta)\approx J_{train}(\theta)\)
- 高方差:
- \(J_{train}(\theta)\)will be low, \(J_{CV}(\theta)\gg J_{train}(\theta)\)

正则化与方差、偏差的关系
正则化可以有效防止过拟合
选择λ的过程:
- Create a list of lambdas (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24});
- Create a set of models with different degrees or any other variants.
- Iterate through the λs and for each λ go through all the models to learn some Θ.
- Compute the cross validation error using the learned Θ (computed with λ) on the$ J_{CV}()$ without regularization or λ = 0.
- Select the best combo that produces the lowest error on the cross validation set.
- Using the best combo Θ and λ, apply it on$ J_{test}()$ to see if it has a good generalization of the problem.
注:训练时带λ,计算各个集的误差时不需要λ,即\(J_{train}(\theta)\)、\(J_{CV}(\theta)\)、\(J_{test}(\theta)\)都不包含正则项 \[ J_{train}(\theta)=\frac {1}{2m}\sum \limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 \]
学习曲线(error-训练集的大小)
- 高偏差
- Low training set size: causes \(J_{train}(\Theta)\) to be low and \(J_{CV}(\Theta)\) to be high.
- Large training set size: causes both \(J_{train}(\Theta)\) and \(J_{CV}(\Theta)\) to be high with \(J_{train}(\Theta)≈J_{CV}(\Theta)\).
- 高偏差,更多训练数据不会有很大帮助

- 高方差
- Low training set size: causes \(J_{train}(\Theta)\) to be low and \(J_{CV}(\Theta)\) to be high.
- Large training set size: \(J_{train}(\Theta)\) increases with training set size and \(J_{CV}(\Theta)\) continues to decrease without leveling off. Also, \(J_{train}(\Theta) < J_{CV}(\Theta)\) but the difference between them remains significant.
- 高方差,更多训练数据可能有帮助

- 高偏差
诊断法则如何判断
- 更多训练数据——高方差,画学习曲线
- 更少特征集避免过拟合——高方差
- 更多特征——高偏差
- 增加多项式特征——高偏差
- 减少(高偏差)或增大正则化参数值(高方差)
- 正则化会保留所有的特征变量,但是会减小特征变量的数量级。正则化就是使用惩罚项,通过惩罚项,我们可以将一些参数的值变小。通常参数值越小,对应的函数也就越光滑,也就是更加简单的函数,因此不容易发生过拟合问题。
- 神经网络很容易过拟合,正则化项非常有用
- 如何选择几层隐藏层:
- 通过交叉验证集,测试1,2,…,l个隐藏层的误差,选择表现最好的一个
- 如何选择几层隐藏层:
Build a Spam Classifier
- 做法:
- 遍历整个训练集,然后在中间选出出现次数最多的n个单词,n一般介于10000和50000之间,作为特征
- 列出可能的做法,讨论可行性,然后选择一个方向
- 误差分析
- 推荐做法:
- 用简单算法快速实现,然后测试CV集(避免过早优化)
- 画学习曲线,决定是否需要更多数据、更多特征或其他
- 误差分析:手动检验CV集中的错误分类样本,发现系统性的错误分类特征,构造更好的特征
- 手动对错误的部分分类
- 发现特征
- 用数字来量化表现误差(在CV集上,不能在test集上)
- 推荐做法:
- stem词干提取(porter stemmer)
- skewed classes 偏斜类问题
- 癌症的比例非常非常低
- 查准率(precision):预测为1的病人里,多少是真正得癌症的
- \(=\frac{True\ positives}{predicted\ positives}=\frac{True\ positives}{True\ pos+False\ pos}\)
- 召回率Recall:实际得癌症的病人里,多少是真正预测得癌症的
- \(=\frac{True\ positives}{actual\ positives}=\frac{True\ positives}{True\ pos+False\ neg}\)
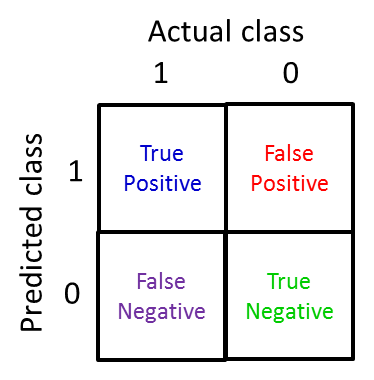
- 假设现在想要预测y=1,当非常自信的情况下(修改\(h_\theta(x)\)分类临界值threshold0.5为0.9):高查准,低召回
- 假设想要避免错过癌症案例,(修改\(h_\theta(x)\)分类临界值0.5为0.3):高召回,低查准
- 绘制查准率-召回率曲线
- \(F_1\)Score \(=\frac{2PR}{P+R}\):
- 评估选择算法或者不同临界值的量化标准
- Data For Machine Learning
- 有大量训练数据可以显著提升算法表现,可能得到低方差、低偏差的结果,test误差和train误差也相近
- 多项式参数对大训练集没有帮助
Related Posts