Machine Learning Week04

Posted on Edited on In Views: Symbols count in article: 1.2k Reading time ≈ 1 mins.

Neural Networks： Representation

1. Non-linear Hypotheses

特征多，有高次项

2. Neural Networks

  1. Model representation

    • bias unit偏置项（=1）

    • sigmoid activation function S型激励函数

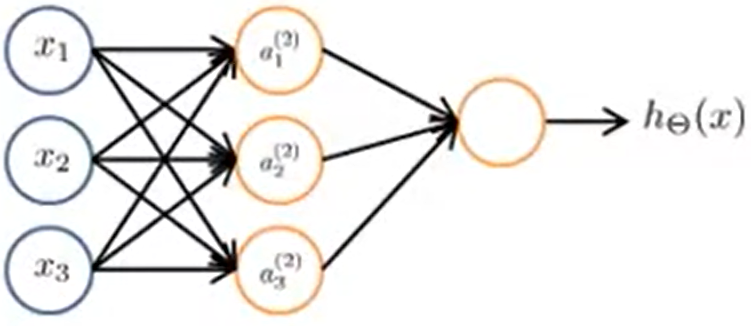
    • input layer —— hidden layer —— output layer

    • \[ a_i^{(j)}= "activation"\ of\ unit\ i\ in\ layer\ j \]

      \(\Theta^{(j)}=\) matrix of weights controlling function mapping from layer j to layer j+1 ，即参数矩阵（波矩阵、权重矩阵）

      如果一个网络在 j 层有\(s_j\)个单元，j+1层有\(s_{j+1}\)个单元，那么\(\Theta^{(j)}\)的矩阵维度是\(s_{j+1}\times(s_j+1)\)，因为要加上bias unit

      神经网络 \[ \begin{array}{r} a_{1}^{(2)}=g\left(\Theta_{10}^{(1)} x_{0}+\Theta_{11}^{(1)} x_{1}+\Theta_{12}^{(1)} x_{2}+\Theta_{13}^{(1)} x_{3}\right)=g(z_1^{(2)}) \\ a_{2}^{(2)}=g\left(\Theta_{20}^{(1)} x_{0}+\Theta_{21}^{(1)} x_{1}+\Theta_{22}^{(1)} x_{2}+\Theta_{23}^{(1)} x_{3}\right)=g(z_2^{(2)}) \\ a_{3}^{(2)}=g\left(\Theta_{30}^{(1)} x_{0}+\Theta_{31}^{(1)} x_{1}+\Theta_{32}^{(1)} x_{2}+\Theta_{33}^{(1)} x_{3}\right) =g(z_3^{(2)}) \\ h_{\Theta}(x)=a_{1}^{(3)}=g\left(\Theta_{10}^{(2)} a_{0}^{(2)}+\Theta_{11}^{(2)} a_{1}^{(2)}+\Theta_{12}^{(2)} a_{2}^{(2)}+\Theta_{13}^{(2)} a_{3}^{(2)}\right) \end{array} \]

    • 即前向传播（forward propagation）

3. Applications

  1. 与运算（-30，20，20）
  2. 或运算（-10，20，20）
  3. 非运算（10，-20）
  4. XNOR运算，同或运算（相同为1，否则为0）：两层神经网络
  5. Multiclass Classification，如果4个分类器结果则例如[0,0,1,0]

​

Related Posts